

CD
hitorri-977
Limited edition of 200
Out on December 13, 2020
Ftarri Bandcamp
Masahide Tokunaga: alto saxophone
Hiroyuki Ura: sine tones
Composed by Taku Sugimoto in 2020
Commissioned by Masahide Tokunaga
Recorded without audience at Ftarri, Tokyo, July 27, 2020
Recorded and mastered by Hiroyuki Ura
Artwork by Taku Sugimoto
Design by Cathy Fishman
Liner notes by Taku Sugimoto (translation by Cathy Fishman and Taku Sugimoto)
When we think about the relationship between two things that had not been given much attention before, or two things with no clear connection, we sometimes make a discovery.
Once I was going to Europe and wanted something to read on the plane, so I bought a book in a bookstore at Narita Airport--Fermat's Last Theorem by Simon Singh (translated by Kaoru Aoki, published by Shinchosha). It's a documentary-style book that can be understood even by people without specialized math knowledge. I've forgotten most of it, but I was excited by a passage stating that Goro Shimura's "Taniyama-Shimura conjecture" (which I couldn't possibly understand or explain mathematically) had been an important key to the proof of Fermat's theorem, although the two had previously been considered unrelated. The exciting thing was that it said that proving the Taniyama-Shimura conjecture had led directly to the proof of Fermat's last theorem.
In the book Noh no mieru fukei (landscapes in Noh) by Tomio Tada (Fujiwara Shoten), Tada (who specialized in immunology) wrote the following about creative research: "It isn't creating something from nothing. As the American psychologist Silvano Arieti said, 'it's succeeding in making a connection between things that had previously been viewed as unrelated.' In this case, 'succeeding' means influencing other researchers and changing their way of thinking. In art, it's touching people's emotions." (p. 99)
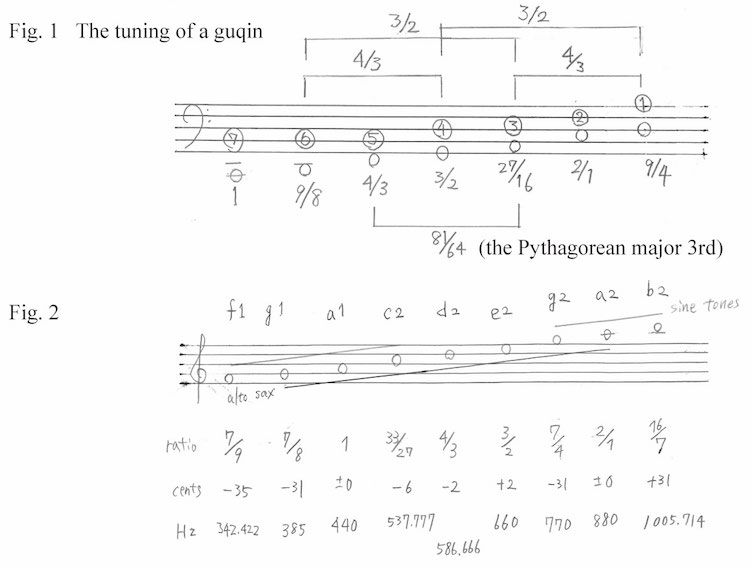
In my case, it's this. About six years ago, my friend Simon Roy Christensen came here from Denmark and showed me a guqin, a type of stringed instrument played in ancient China. The tuning, starting from the lowest string, was C, D, F, G, A, C, D. I thought, OK, the open strings are tuned with Pythagorean tuning. (Fig. 1) That's factually correct, but the body of the instrument has markings that serve as kandokoro (fingerboard guides) placed at points down the length of the strings based on distributions of eight, six and five divisions, and at these points the strings are pressed, or lightly brushed with the fingers to create harmonics. A pitch produced by pressing 5/6 of the string length (a minor third higher than the open string) in the case of six divisions, and a pitch of 5/8 of the string length (a minor sixth higher than the open string) in the case of eight divisions, are not included in Pythagorean tuning. (Harmonics produced by touching those nodes are as follows: an octave higher or an octave and a perfect fifth higher than the open string in the six divisions; and one, two or three octaves higher than the open string in eight divisions.) None of the pitches produced from the five divisions are included in Pythagorean tuning: 4/5 is a major third higher (5/4); 3/5, a major sixth higher (5/3); 2/5, an octave and a major third higher (5/2); and 1/5, two octaves and a major third higher (5/1). Any harmonics produced with those nodes are two octaves and a major third higher (5/1).*1 If you play 3/5 of the seventh string (the lowest [C] string), you will get an A of 5/3. This tone is slightly different in pitch from the open third string, which is 27/16. It's theoretically the same as the tone produced by playing 4/5 of the fifth (F) string (the major third in Pythagorean tuning is 81/64). In this way, a number of tones that are not included in Pythagorean tuning are produced from the points of the five divisions.
What I've just described is very interesting, and it's influenced my composing. But my "discovery" was somewhere else--in the arrangement of sounds on the open strings of the guqin. The main Japanese music scales are the ritsu scale, used in gagaku and Buddhist chanting, and the minyo (folk music) scale, used in folk songs and children's songs. (Other scales are the Miyako-bushi scale and Okinawa scale, both of which include half-tones.) On the guqin, the arrangement of notes from the seventh to the second strings (C, D, F, G, A, C) are the ritsu scale, and the arrangement of notes from the sixth to the first strings (D, F, G, A, C, D) are the minyo scale. But this may not be an important discovery. First of all, on the open strings of the guqin, the component notes (leaving aside octaves) are the same, so the question is what the differences are. This will be discussed below. Secondly, although quite a bit of Japanese music combines various scales, I have never seen tuning that could be interpreted as a mix of two scales on a single instrument. Thirdly, since a scale played on an actual guqin includes the notes in the five divisions, it's probably more a mixture of Pythagorean tuning and five-limit just intonation than a combination of the ritsu and minyo scales. Thus, it's far removed from Japanese scales.*2 On the other hand, I'm not a researcher. Initially, I thought for years about creating "(Japanese) music that could possibly have existed," based on the hypothesis that the ritsu and minyo scales might have started out as a single scale. However, while making the open string scales of the guqin the main focus, I thought of changing some of the notes in those scales to different whole number ratio intervals and adding different notes, thereby creating music mixing the ritsu, minyo, I-don't-know-what scales. The scales on the guqin are a mixture of Pythagorean tuning and five-limit just intonation. My composition this time is a mixture of ritsu and minyo scales and seven-limit just intonation (I did not use five-origin notes).
Tokunaga's music on sax has the same scale as the open strings of the guqin, but the range was decided by actually listening to his sax playing. For the sine tones as well, only seven pitches are used, but there are two pitches which are not produced by the sax, and the sax has two pitches not produced by sine tones. (Fig. 2) The reason I used notes of seven-limit just intonation is that I meant to narrow the minor third interval and widen the major third with [G]s an octave apart on the sax, and with the sine tone F and B. Neither F nor B is part of the ritsu or minyo scale. These intervals have the aim of dislocating the ritsu/minyo scales played by the sax. Japanese scales have "nuclear tones" which function something like keynotes (tonic notes) in western music. The nuclear tones of the ritsu scale are G and D in this composition's intervals, and those of the minyo scale are A and D. The difference between these nuclear tones is the difference between the two scales. However, leaving the minyo scale aside, the ritsu scale is not something very familiar to my sense of sound, honestly speaking. Therefore, I purposely created all the sax melodies in my head, without using an instrument or thinking consciously about the nuclear tones; and while there is a certain minyo scale feeling, there is hardly anything reminiscent of the ritsu scale. In the sine tone intervals I placed importance on G, which is one of the nuclear tones of the ritsu scale, and B, which is unrelated to both the ritsu and the minyo scale. By combining this with the sax melodies, I intended to kill two birds with one stone and express the ritsu and "I-don't-know-what" scales. But I probably managed to shoot down just one bird--the "I-don't-know-what" bird.
But I had another aim, too--difference tones. This is the phenomenon whereby one hears the sound produced by the difference in frequencies. As an example, in the case of the intervals used this time, the difference tone between G (770 Hz) and 660 Hz is A (110 Hz). It's said to be easier to hear difference tones when sounds have few harmonic components. Of course, sine tones don't produce harmonics. Tokunaga's sax doesn't have many high-order harmonics either. Additionally, the register used is on the high side. (In my experience, it's often easier to hear difference tones between high sounds.) The designation of the sax's microtones is only the target value of effort. When the harmonic level of two sounds is high, it means that, for example in the case of fundamental tones and 3/2, the third overtone of the fundamental tone matches the second overtone of 3/2. When this overtone starts to shift, the groaning sound becomes intense. In this composition, I did my utmost to avoid this kind of interference between overtones. Other than octaves, I got rid of the harmonic levels of pitches, and prioritized difference tones. Where groaning can occur is in the intervals where it's possible for the sax and sine tones to be in unison: 7/8 (G), 1 (A), 33/27 (C), 7/4 (G), and 2/1 (A). Of these intervals, 7/4 (G) and 2/1 (A) are second overtones of 7/8 (G) and 1 (A) on the sax (an octave higher), so groaning can occur as a result of these overtones and sine tones. Of course, third-and-over overtones undoubtedly come out of the sax, but these are all higher than the highest notes of the sine tones, so they are unrelated to the groaning. Therefore, in this recording as well, groaning results only when the sax and sine tones are in unison or in an octave relationship, as mentioned above.
The sax has melodic patterns from a to p, and the sine tones have melodic patterns from a to s, with a being the longest and p or s the shortest. Each musician plays these melodies in the order they prefer, and when one melody is finished, they have to rest for about the same duration of time as the melody. In this recording, I determined sine tone order through chance operations, and here and there I applied portamento to the notes. At the same time, Tokunaga played in order from top to bottom or from bottom to top. (by Taku Sugimoto)
*1 The pitch which is produced by pressing the point at 4/5 of the length of an open string is the inverse of the pitch of the open string, in other words 5/4. In the case of harmonics, this is easy to understand if one uses the guitar as an example. First, the harmonic point of 1/2 is 2/1 on the twelfth fret, 1/3 is 3/1 on the seventh fret, 1/4 is 4/1 on the fifth fret, and 1/6 is 3/1 on the third fret (just past it towards the bridge). These harmonic points are also in a symmetrical position on the bridge side, with the twelfth fret as the center. 1/5 is at the ninth and fourth frets and their points of symmetry; and since there is no harmonic point at the octave location, everything is 5/1 (however, the timbres are quite different). It would take too much space to explain the ways of translating pitches expressed by these whole number ratios into general intervals and pitch names, so I will write just a little about the simplest method--that is, memorizing harmonic series. For example, 3/2 is the same as the interval between the second and third harmonic overtones. On the guitar, it's the interval between the harmonics of the twelfth and seventh frets.
*2 However, since the Miyako-bushi and Okinawan scales include half-tones, it could include five-limit (or over) just intonation.
Masahide Tokunaga, who was born in 1982 and lives in Tokyo, is an alto sax player and improviser with a unique and original playing style. He has released two improvisation CDs on the Hitorri label: Alto Saxophone 2 (2015) and Bwoouunn: Fleeting Excitement (2017). For his next solo album Tokunaga planned to engage with composed works, and thus he decided to commission a composition from Taku Sugimoto.
Guitarist Taku Sugimoto has long been active as a composer as well. He is currently regarded as one of the most important composers on the experimental/improvised music scene, particularly in Europe and North America. After receiving Tokunaga's commission, Sugimoto first turned his attention to Japanese musical scales, then wrote a piece for sax and sine tones based on his inquiry into these scales. In this composition Sugimoto also focuses on difference tones (the sonic phenomenon resulting from the difference between two frequencies).
On July 27, 2020, Tokunaga made a recording (without audience) along with Hiroyuki Ura at Ftarri, with Sugimoto in attendance. (Tokunaga played alto sax and Ura played sine tones.) The approximately hour-long performance that took place that day is divided into two tracks of 34 and 26 minutes on this CD. Throughout, the performance is simple and pure and proceeds in a quiet way. At the same time, Sugimoto's compositional intentions and even Tokunaga's resolution in carrying out a new endeavor seem to come through in the sound. It's a fascinating performance. The CD includes detailed liner notes (in Japanese and English) by Taku Sugimoto.
